Hoe Bereken Je Een Driehoek: Eenvoudige Stappen Uitgelegd!

Hoe bereken je een driehoek?

Een driehoek is een van de meest elementaire vormen in de meetkunde. Het bestaat uit drie zijden en drie hoeken. In deze gids zullen we je stap voor stap laten zien hoe je een driehoek kunt berekenen en verschillende eigenschappen van een driehoek kunt bepalen, zoals de zijden, oppervlakte en hoeken. Of je nu een student bent die bezig is met wiskunde of een doe-het-zelver die een driehoekige constructie wil maken, deze gids zal je helpen om de berekeningen correct uit te voeren.

1. Bereken de zijden van een driehoek

Om de zijden van een driehoek te berekenen, moet je enkele gegevens hebben. Als je de lengte van twee zijden van een driehoek hebt, kun je de lengte van de derde zijde berekenen met behulp van de stelling van Pythagoras. Deze stelling stelt dat in een rechthoekige driehoek, het kwadraat van de hypotenusa (de zijde tegenover de rechte hoek) gelijk is aan de som van de kwadraten van de andere twee zijden.

Als je bijvoorbeeld de lengte van de twee rechthoekszijden hebt (a en b), dan kun je de lengte van de hypotenusa (c) vinden met behulp van de volgende formule:

c² = a² + b²

Hieruit kun je c berekenen door de vierkantswortel van beide zijden te nemen:

c = √(a² + b²)

Als je de zijden van een niet-rechthoekige driehoek wilt berekenen, moet je andere gegevens hebben, zoals de lengte van de drie zijden of de lengte van een zijde en de bijbehorende hoeken. In dat geval kun je verschillende methoden gebruiken, zoals de wet van cosinus of de wet van sinus, om de lengtes van de zijden te bepalen.

2. Bereken de oppervlakte van een driehoek

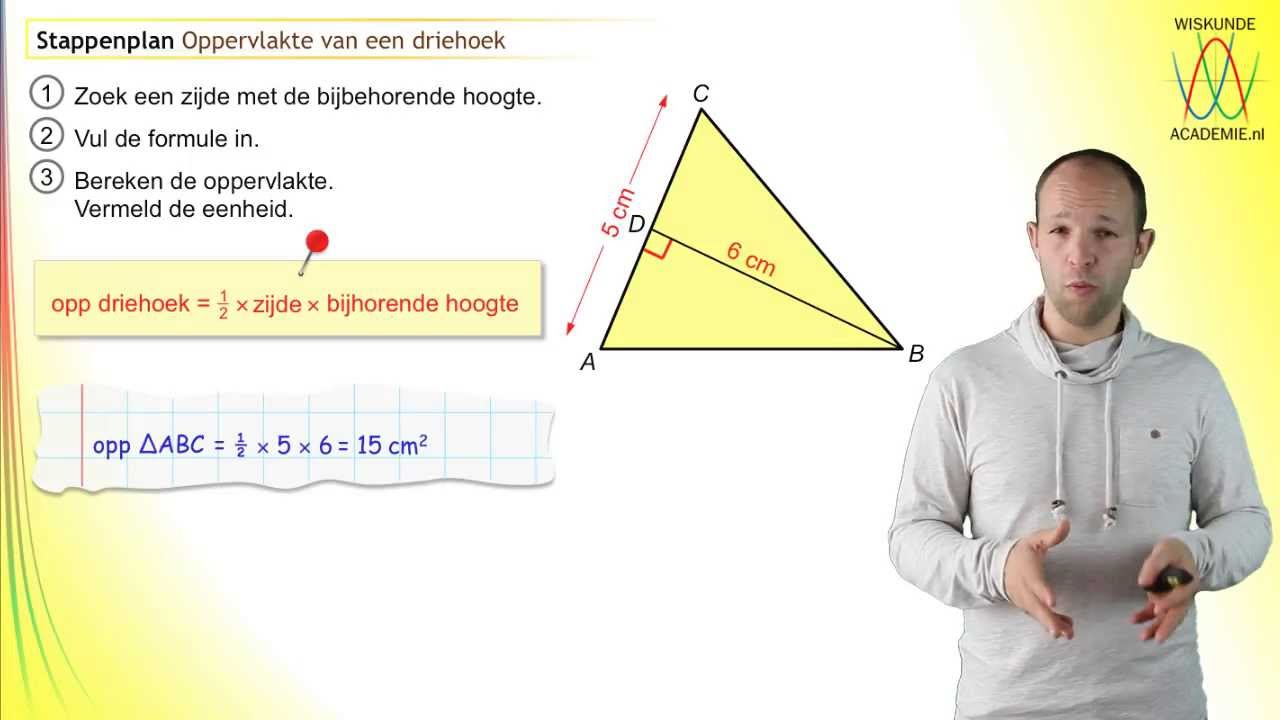
De oppervlakte van een driehoek is het gebied binnen de driehoek. Om de oppervlakte van een driehoek te berekenen, heb je de lengte van de basis en de hoogte nodig. De basis van een driehoek is een van de zijden, en de hoogte is de verticale afstand van de basis naar de top van de driehoek.

De formule om de oppervlakte van een driehoek te berekenen is:

Oppervlakte = (basis × hoogte) / 2

Je kunt de oppervlakte van een driehoek berekenen door de lengte van de basis en de hoogte in te vullen in deze formule. Als je de lengte van de zijden kent, kun je ook de oppervlakte berekenen met behulp van de formule van Heron:

Oppervlakte = √(s × (s – a) × (s – b) × (s – c))

Hierbij is s de halve omtrek van de driehoek en a, b en c zijn de lengtes van de zijden.

3. Bereken de omtrek van een driehoek

De omtrek van een driehoek is de totale lengte van de zijden van de driehoek. Om de omtrek van een driehoek te berekenen, hoef je alleen de lengtes van de zijden op te tellen.

Omtrek = a + b + c

Hierbij zijn a, b en c de lengtes van de zijden van de driehoek.

4. Bereken de hoeken van een driehoek

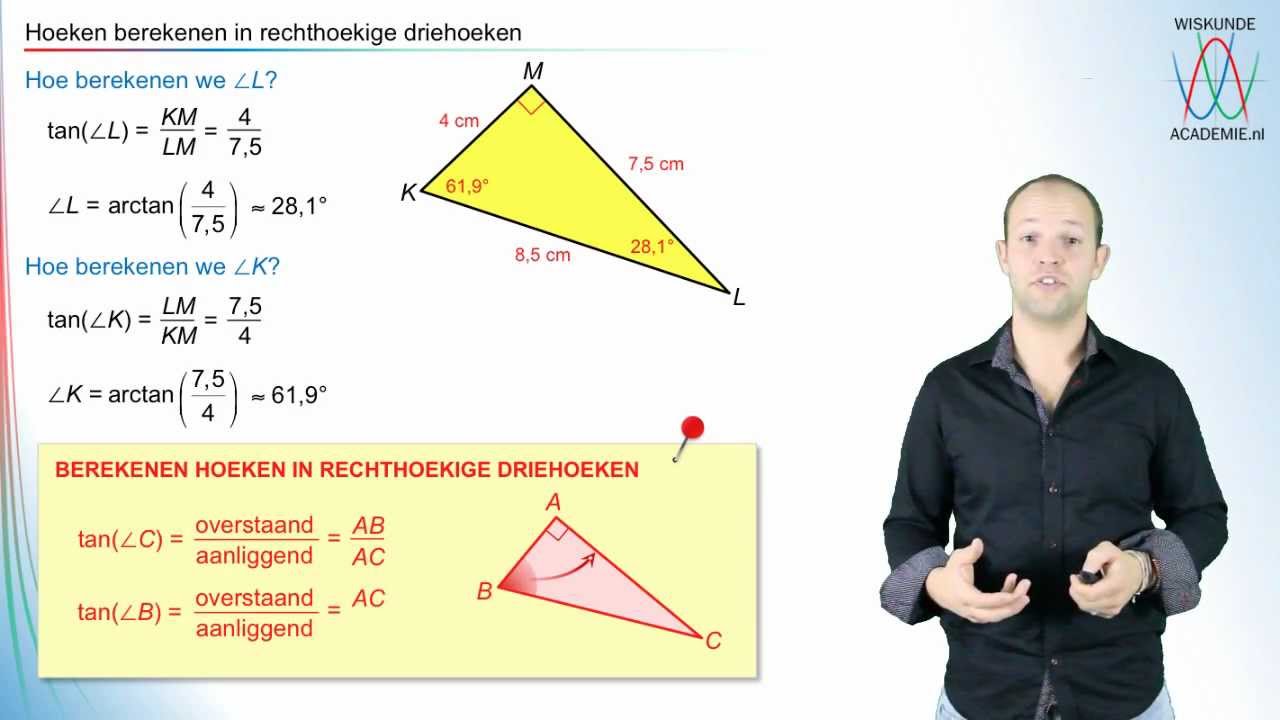
Om de hoeken van een driehoek te berekenen, heb je verschillende gegevens nodig, zoals de lengtes van de zijden of de lengte van een zijde en de bijbehorende hoeken. Er zijn verschillende methoden om de hoeken van een driehoek te berekenen, afhankelijk van de beschikbare gegevens.

Als je bijvoorbeeld de lengtes van de drie zijden hebt, kun je de hoeken berekenen met behulp van de wet van cosinus:

cos(A) = (b² + c² – a²) / (2bc)
cos(B) = (a² + c² – b²) / (2ac)
cos(C) = (a² + b² – c²) / (2ab)

Hierbij zijn A, B en C de hoeken van de driehoek, en a, b en c zijn de lengtes van de zijden.

Als je de lengte van een zijde en de bijbehorende hoek hebt, kun je de andere zijden en hoeken berekenen met behulp van de wet van sinus:

a / sin(A) = b / sin(B) = c / sin(C)

5. Gebruik de stelling van Pythagoras bij rechthoekige driehoeken

De stelling van Pythagoras is een belangrijk concept bij het werken met rechthoekige driehoeken. Een rechthoekige driehoek heeft één hoek van 90 graden. Volgens de stelling van Pythagoras is de som van de kwadraten van de lengtes van de twee rechthoekszijden gelijk aan het kwadraat van de lengte van de hypotenusa.

De formule van de stelling van Pythagoras is:

a² + b² = c²

Hierbij zijn a en b de lengtes van de rechthoekszijden, en c is de lengte van de hypotenusa.

Met behulp van de stelling van Pythagoras kun je de ontbrekende zijde berekenen als je de lengtes van twee zijden kent, of je kunt de zijde controleren als je de lengtes van de andere twee zijden kent.

6. Bereken speciale vormen van driehoeken

Er zijn verschillende speciale vormen van driehoeken, zoals de gelijkbenige driehoek en de gelijkzijdige driehoek, die unieke eigenschappen hebben.

– Een gelijkbenige driehoek heeft twee zijden van gelijke lengte. Je kunt de lengtes van de zijden van een gelijkbenige driehoek berekenen door de stelling van Pythagoras toe te passen en de zijden te vergelijken.

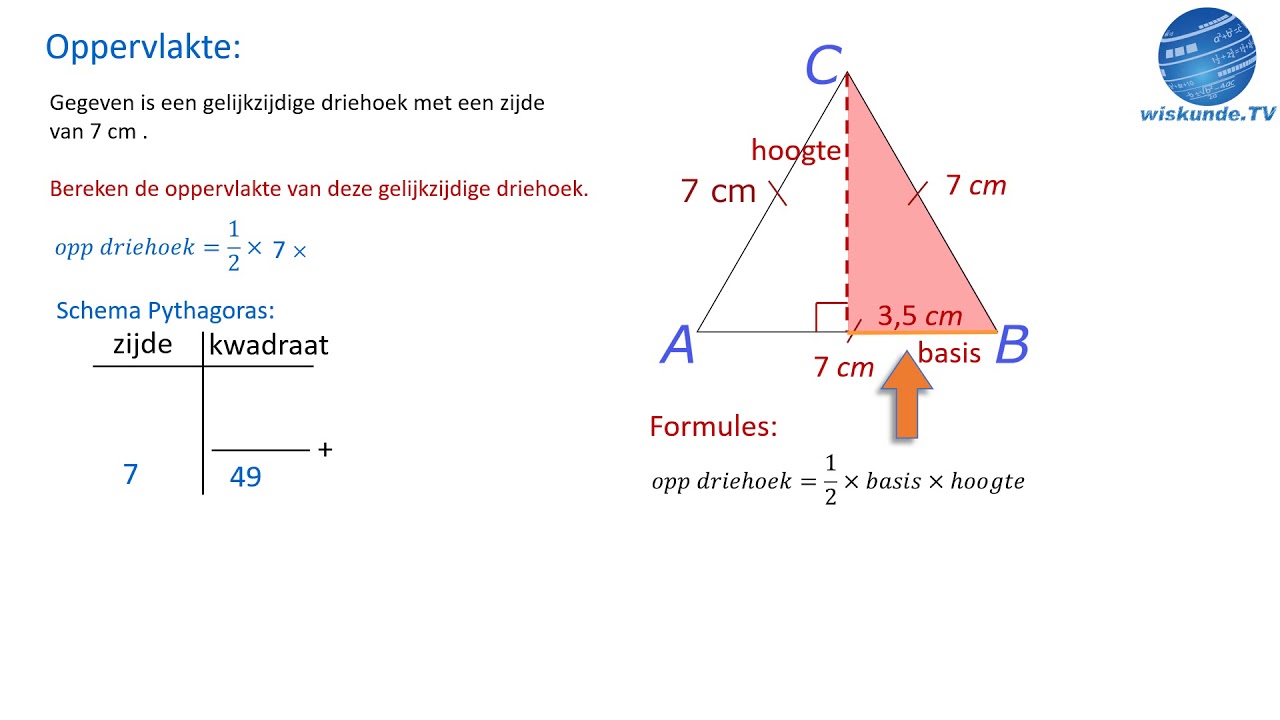
– Een gelijkzijdige driehoek heeft alle zijden van gelijke lengte. Om de lengtes van de zijden van een gelijkzijdige driehoek te berekenen, kun je de driehoek in twee gelijke rechthoekige driehoeken verdelen en de stelling van Pythagoras gebruiken.

Als je de hoeken van een driehoek wilt berekenen, kun je gebruikmaken van een hoekberekeningscalculator of een app die speciaal is ontworpen voor het berekenen van gradenhoeken. Deze hulpmiddelen kunnen je helpen om snel en nauwkeurig de hoeken van een driehoek te berekenen.

Als je de schuine zijde van een driehoek wilt berekenen, kun je een online schuine zijde berekeningshulpmiddel gebruiken. Deze hulpmiddelen vragen om de lengtes van de twee andere zijden en geven je de lengte van de schuine zijde.

Het berekenen van de oppervlakte van een driehoek kan soms lastig zijn, vooral als de vorm van de driehoek complex is. In dat geval kun je gebruikmaken van online oppervlakteberekeningshulpmiddelen die de formules voor driehoekige oppervlakteberekeningen toepassen.

Met al deze berekeningen kun je de eigenschappen van een driehoek bepalen en nauwkeurige metingen krijgen voor je wiskundige problemen of bouwprojecten.

FAQs

1. Hoe bereken je de schuine zijde van een driehoek?

Om de schuine zijde van een driehoek te berekenen, heb je de lengtes van de twee andere zijden nodig. Je kunt een online schuine zijde berekeningshulpmiddel gebruiken om snel en nauwkeurig de lengte van de schuine zijde te vinden.

2. Hoe bereken je een driehoek met 1 zijde en 1 hoek?

Om een driehoek met één zijde en één hoek te berekenen, moet je de lengte van de zijde en de grootte van de hoek kennen. Met behulp van de wet van de sinus kun je de lengtes van de andere zijden berekenen en de bijbehorende hoeken bepalen.

3. Hoe bereken je gradenhoeken?

Je kunt gradenhoeken berekenen met behulp van een hoekberekeningscalculator of een app die speciaal is ontworpen voor het berekenen van hoeken. Deze tools vragen om de lengtes van de zijden en geven je de hoeken van de driehoek.

4. Wat is een hoekberekeningscalculator?

Een hoekberekeningscalculator is een hulpmiddel waarmee je de hoeken van een driehoek kunt berekenen op basis van de lengtes van de zijden. Je voert de lengtes van de zijden in en het hulpmiddel geeft je de hoeken van de driehoek.

5. Hoe bereken je een gelijkbenige driehoek?

Om een gelijkbenige driehoek te berekenen, moet je weten dat deze twee zijden van gelijke lengte heeft. Je kunt de lengtes van de zijden van een gelijkbenige driehoek berekenen door de stelling van Pythagoras toe te passen en de zijden te vergelijken.

6. Hoe bereken je de schuine zijde online?

Je kunt online schuine zijde berekeningshulpmiddelen gebruiken om de lengte van de schuine zijde van een driehoek te berekenen. Deze hulpmiddelen vragen om de lengtes van de twee andere zijden en geven je de lengte van de schuine zijde.

7. Is er een app om gradenhoeken te berekenen?

Ja, er zijn verschillende apps beschikbaar waarmee je gradenhoeken kunt berekenen op basis van de zijden van een driehoek. Deze apps vragen om de lengtes van de zijden en geven je de hoeken van de driehoek.

8. Hoe bereken je de oppervlakte van een driehoek?

Om de oppervlakte van een driehoek te berekenen, moet je de lengte van de basis en de hoogte kennen. De formule om de oppervlakte van een driehoek te berekenen is (basis × hoogte) / 2. Je kunt ook de formule van Heron gebruiken als je de lengtes van de zijden kent.

In conclusie, het berekenen van een driehoek kan soms uitdagend lijken, maar met de juiste formules en methoden is het goed te doen. Of je nu de zijden, oppervlakte, omtrek of hoeken van een driehoek wilt berekenen, deze gids biedt je stapsgewijze instructies en handige tips om het proces soepel te laten verlopen. Vergeet niet om de beschikbare online hulpmiddelen en apps te gebruiken om je berekeningen te verifiëren en nauwkeurige resultaten te krijgen.

Een rechthoekige driehoek heeft 3 zijdes: 2 rechthoekszijden en een schuine zijde. De schuine zijde wordt ook wel eens de langste zijde, of de hypotenusa genoemd. Bij de stelling van Pythagoras kan je de schuine zijde berekenen wanneer je de 2 rechthoekszijden weet. De stelling wordt vaak aangegeven als a² + b² = c².De oppervlakte O van een driehoek is gelijk aan het halve product van de lengte van een zijde en de lengte van de hoogtelijn op die zijde. Anders geformuleerd: oppervlakte = basis × halve hoogte.Oppervlakte driehoek

De oppervlakte van de driehoek reken je de basis x de hoogte x 0.5. Omdat een driehoek de helft is van een rechthoek moet je dit delen door 0.5. De hoogte is vanzelfsprekend bij een rechthoekige driehoek, maar bij een driehoek die geen rechthoek heeft is dat moeilijk te vinden.

Wat Is De Formule Van Een Driehoek?

Hoe Oppervlakte Berekenen Van Driehoek?

Hoe Bereken Ik De Zijde Van Een Driehoek?

Hoe Bereken Je Gelijkzijdige Driehoek?

Delen 36 hoe bereken je een driehoek